In this example, we are going to solve for a statically indeterminate frame using slope-deflection equation. The solution procedure is similar to that for beam, except we need to consider whether the frame will experience sidesway based on its configuration, loading, material variability ad support condition.
The frame is first segmentized span by span, and the convention of internal moment is set for both ends of each member. These individual members are classified based on the end conditions and presence of end moments. Suitable slope-deflection equation is then adopted for each of the unknown end moment.
Readily available fixed end moment (FEM) formula is used to determine the unknown FEM in the slope-deflection equation. This frame is symmetrical and thus it will not experience sidesway. Therefore, we can eliminate the unknown span end displacement. For unrestrained node i.e. B and C, the rotation unknown should be remained.
After all the parameters are determined, we construct equilibrium equations containing all unknowns. We can calculate the unknowns by solving these simultaneous equations.
The following introduces the solution of symmetrical frame using slope-deflection equation. Watch the video above for full details.
Frame overview
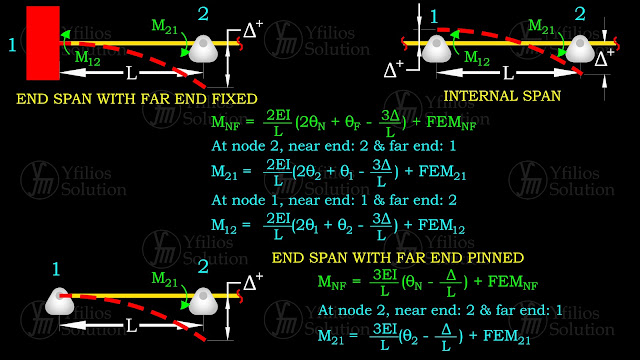
Slope deflection equation based on span type
Implementation of slope deflection equation in the example
Application of FEM in the example
Sidesway and non-sidesway frame overview
Elimination of span end displacement parameter
Simplification of equations based on boundary condition
Solution for simultaneous equations
Solution for internal moment












0 Comments